A personal website about me navigating the World of AI from a Statistical Mechanics viewpoint, reviewing software engineering that I found useful and other interesting updates.

© 2022. All rights reserved.
The NML coarse grained method utilizes a normal mode decomposition of the dynamical space to achieve large numerical step size. Our first paper ‘Normal Mode Partitioning of Langevin Dynamics for Biomolecules’ authored by Christopher R. Sweet, Paula Petrone, Vijay S. Pande and Jesus A. Izaguirre was published in the Journal of Chemical Physics. It established the basic principles and theory of the method, and the corresponding informational website can be found here. To implement an efficient realization has required further work on Hessian diagonalization and Langevin methods for large step size.
The basic idea is that the maximum timestep is dependent on the highest frequency in the system, but these high frequency vibrations contribute little to the dynamics of interest. By removing frequencies above a given threshold large timesteps can be used, and the high frequencies are ‘relaxed’ by minimization.
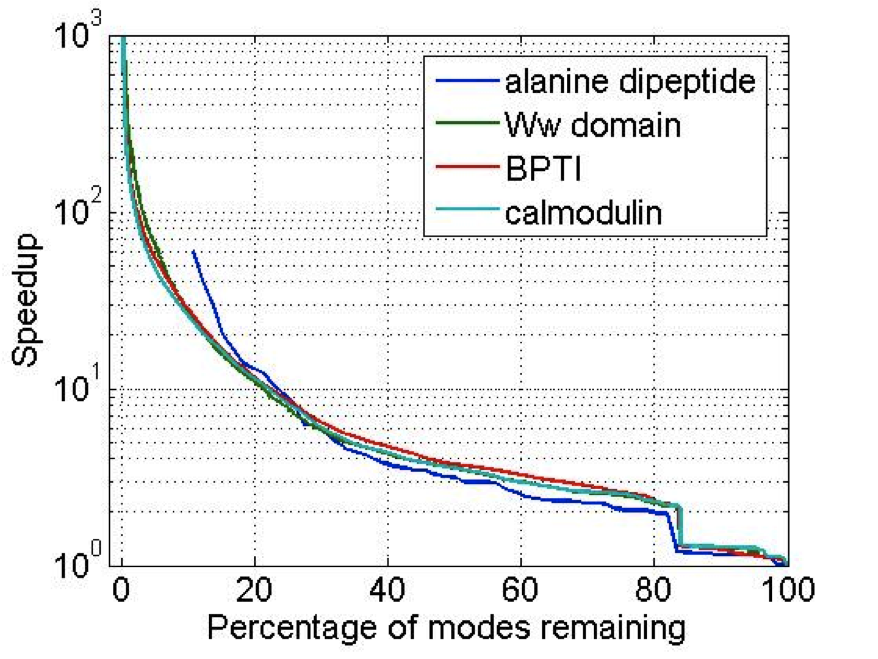
The coarse-graining strategy to computing the frequency partitioning is to find a reduced set of normalized vectors that spans the low frequency space of interest. The quadratic product of these vectors and the Hessian, which can be done in \(O(N)\) due to their block structure, produces a small matrix which is cheap to diagonalize as seen below. This avoids the \(O(N^{3})\) cost of traditional diagonalization, instead the cost is \(O(N^{9/5})\).
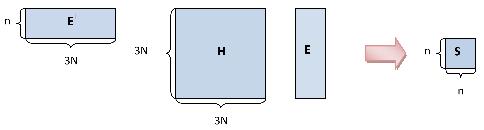
The following graphic depicts the block structure of the Hessian that is used to allow an efficient diagonalization method.
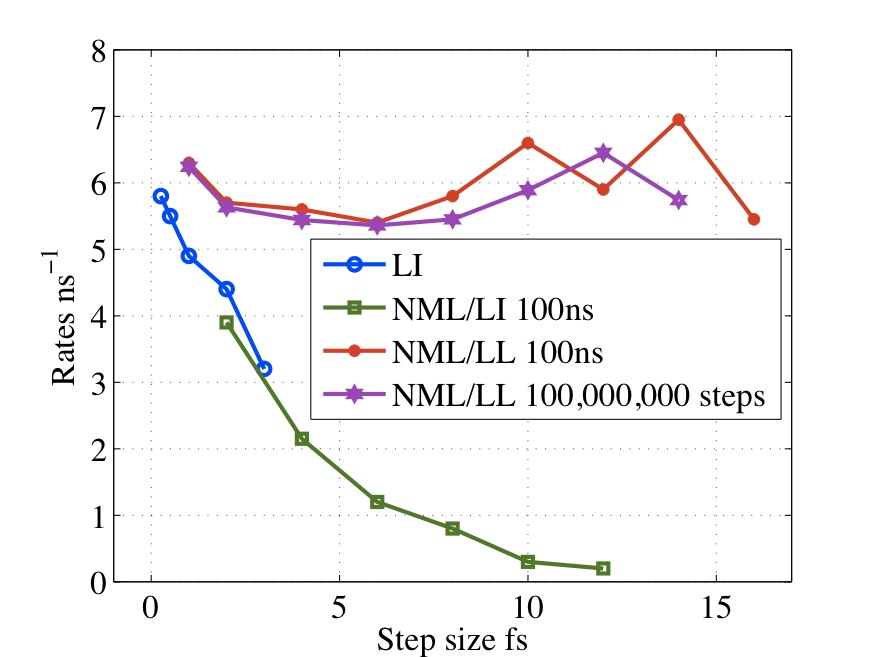
Traditional Langevin thermostats give large error at large values of (time-step*damping coefficient) Methods such as Langevin Impulse alleviate many of these problems but has been found to overdamp for large time-steps. We have derived a method based on the leapfrog which exactly integrates the velocities over the half step. This has been shown to give exact results for isomerization rates for alanine dipetide with step sizes from 0.25 to 12fs.
The system will be time-propagated using the Langevin equation and the final equations for propagation are as follows. If we assume \(\mathrm{t}=0\) at initial velocity \(\mathbf{v}^n,\) initial positions \(\mathbf{x}^n\) and \(\mathrm{t}=\Delta t/2\) at \(\mathbf{v}^{n+\frac{1}{2}}\) then
\[\begin{align} \mathbf{v}^{n+\frac{1}{2}} =&e^{-\gamma \frac{\Delta t}{2}}\mathbf{v}^n+\left(\frac{1-e^{-\gamma \frac{\Delta t}{2}}}{\gamma}\right)\mathbf{M}^{-1}\mathbf{f}(\mathbf{x}^n)+ \\ &\sqrt{2k_{\mathrm{B}}T\gamma}\,\mathbf{M}^{-\frac{1}{2}}\sqrt{\frac{1-e^{-\gamma \Delta t}}{2\gamma}}\mathbf{Z}^n, \end{align}\]for random variable \(\mathbf{Z}^n\) with zero mean and unit variance. Positions can be found from
\[\begin{align} \mathbf{x}^{n+1} = \mathbf{x}^{n} + \Delta t~ \mathbf{v}^{n+\frac{1}{2}}, \end{align}\]and finally the remaining half step for the velocities
\[\begin{align} \mathbf{v}^{n+1} =& e^{-\gamma \frac{\Delta t}{2}}\mathbf{v}^{n+\frac{1}{2}}+\left(\frac{1-e^{-\gamma \frac{\Delta t}{2}}}{\gamma}\right)\mathbf{M}^{-1}\mathbf{f}(\mathbf{x}^{n+1})+ \\ &\sqrt{2k_{\mathrm{B}}T\gamma}\,\mathbf{M}^{-\frac{1}{2}}\sqrt{\frac{1-e^{-\gamma \Delta t}}{2\gamma}}\mathbf{Z}^{n+1}, \end{align}\]for random variable \(\mathbf{Z}^{n+1}\), again with zero mean and unit variance.
My interest is to modeling multi-cellular systems using sub-cellular elements (SCEM). In contrast to the Cellular Potts models (CPM), a dynamical system is developed that defines cellular shape and elasticity, by emulating the cytoskeleton, and uses the Lennard-Jones potential, to mimic cellular adhesion, giving more realistic simulations. The current methods use harmonic restraints between the sub-cellular elements (SCE) to give the correct shape and elasticity, extensions of the model to cell division allows the restraint to be removed beyond a given distance. A schematic representation for two cells, i and j can be seen in Figure 1, where the internal (cytoskeleton) and external (adhesion) forces are shown.
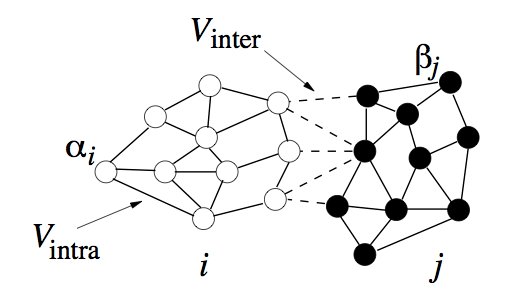
Since the SCEM method derives a biologically relevant potential, the inter SCE forces can be found by taking the derivative w.r.t. the positions.
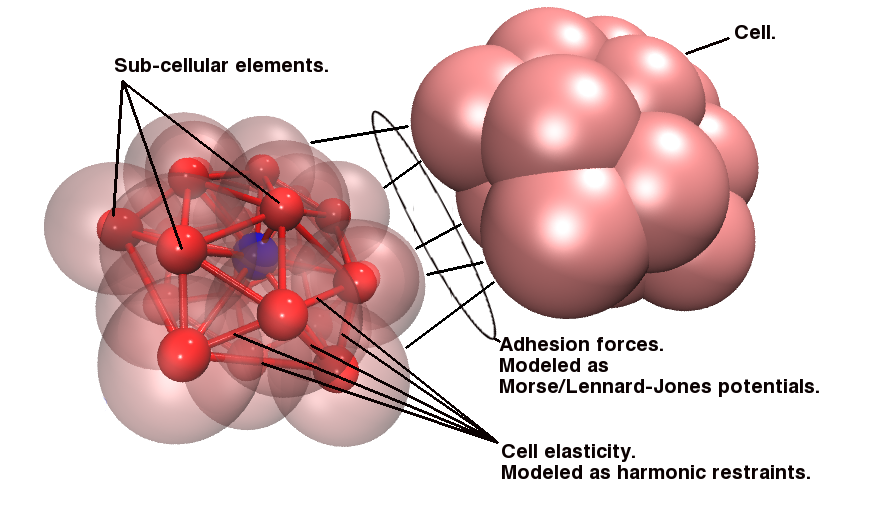
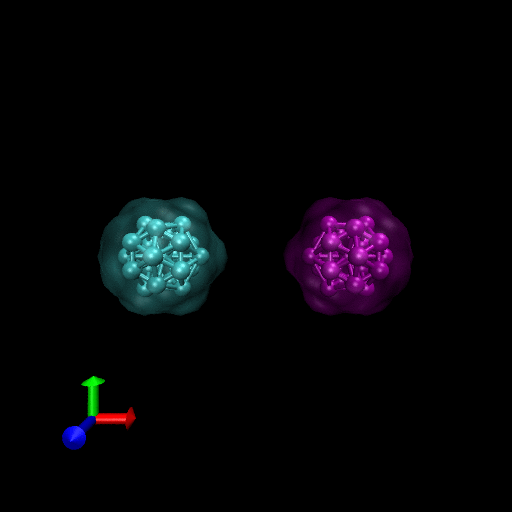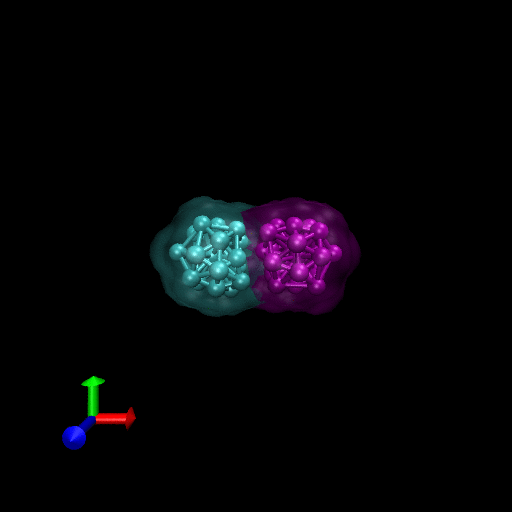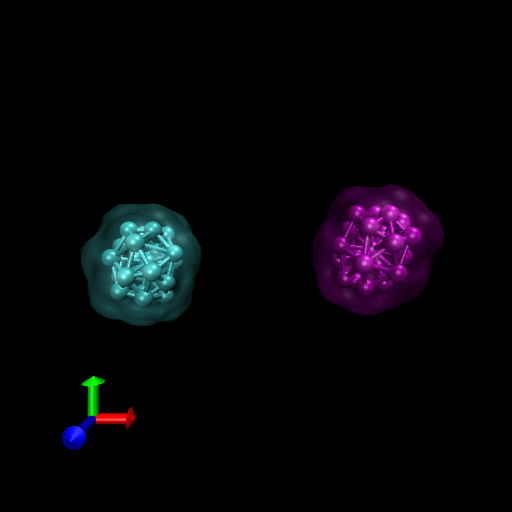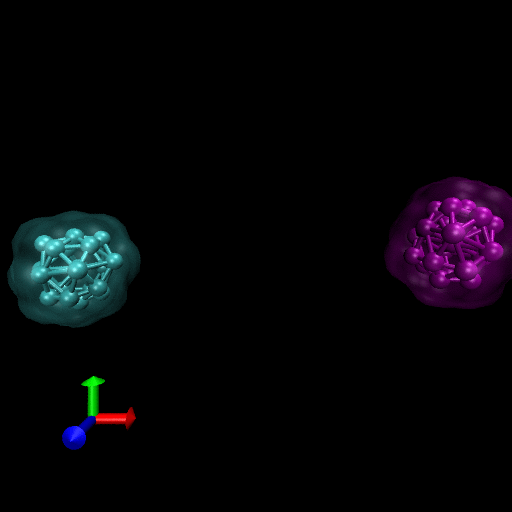
Since the blood cells and platelets are not expected to divide we propose to model the cells using a central SCE connected to SCE representing the surface of the cell, by harmonic restraints. The surface SCE will be coupled to their nearest surface neighbors by harmonic restraints. The length and ‘stiffness’ of the restraints will define the shape and elasticity of the cells. The Figure below depicts our proposed cell structure, the blue SCE represents the center of the cell and the surface is defined by the red SCE. The transparent spheres show the effective Lennard-Jones or Morse potential minima where the effective cell surface is defined (the minimum potential energy corresponding to the cell adhesion value). The cell consists of 21 SCE in this representation, and is rendered using VMD and psf/pdb files generated for the cell.
We have simulated collisions and flow coupling to prove the relevant concepts as seen in the following Figures for Platelets and Blood cells.


Our collaboration with the OpenMM group at Stanford University has allowed me to implement a GPU version of the Normal Mode Langevin method in OpenMM. This GPU library is freely available and Protomol has been extended to utilize OpenMM.
Collaboration between LCLS group at Notre Dame and Robert D. Skeel at Purdue University.
Hybrid Monte Carlo (HMC) is a rigorous sampling method that uses molecular dynamics as a global Monte Carlo move, but the acceptance rate of HMC decays exponentially with system size. The Shadow Hybrid Monte Carlo (SHMC) was previously introduced to overcome this performance degradation by sampling instead from the shadow Hamiltonian defined for MD when using a symplectic integrator. SHMC’s performance is limited by the need to generate momenta for the MD step from a non-separable shadow Hamiltonian. To overcome this we have introduced the Separable Shadow Hamiltonian Hybrid Monte Carlo (S2HMC) method, based on a formulation of the leapfrog/Verlet integrator that corresponds to a more separable shadow Hamiltonian, which allows efficient generation of momenta. S2HMC gives the acceptance rate of a 4th order integrator at the cost of a 2nd order integrator. The first paper was published in the Journal of Chemical Physics, Fall 2009.
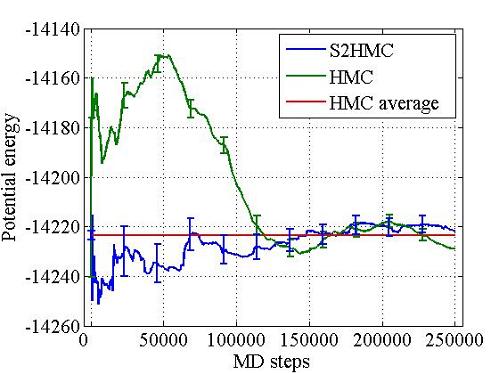
Collaboration with Ben Leimkuhler at Edinborough University and Eric Barth at Kalamazoo College.
During the final two years I studied the thermostatting of dynamical systems in order to generate simulations which sample from the Gibbs, or canonical, ensemble. Molecular dynamics trajectories that sample from this distribution can be generated by introducing a modified Hamiltonian with additional degrees of freedom as described by Nose. To achieve the ergodicity required for canonical sampling, a number of techniques have been proposed based on incorporating additional thermostatting variables, such as Nose-Hoover chains. For Nosé dynamics, it is often stated that the system is driven to equilibrium through a resonant interaction between the self-oscillation frequency of the thermostat variable and a natural frequency of the underlying system. By pioneering the introduction of multiple thermostat Hamiltonian formulations, which are not restricted to chains, it has been possible to clarify this perspective, using harmonic models, and exhibit practical deficiencies of the standard Nose-chain approach. As a consequence of this it has been possible to propose a new powerful “recursive thermostatting” procedure which obtains canonical sampling without the stability problems encountered with chains. This method also has the advantage that the choice of Nose mass is essentially independent of the system to be thermostatted. In addition a Hamiltonian chains method, Nosé-Poincare chains, has been proposed where these methods are appropriate. This research has yielded two papers, “The Canonical Ensemble via Symplectic Integrators using Nose and Nosé-Poincaré chains” which has been accepted for publication by the Journal of Chemical Physics, and the more recent “A Hamiltonian Formulation for Recursive Multiple Thermostats in a Common Timescale” which has been submitted for publication. As an aid to understanding these methods I have created a website where the methods can be compared which can be accessed via the “Recursive Thermostatting simulation” link to the left. This site uses a cgi script to integrate the simulation for the specified time and return images of the resulting thermostat variable phase-space, distributions and averaged local kinetic energy.

Thanks for reading!